实习十五　相关回归分析

　　一、目的意义

　　1．掌握直线相关与回归分析的意义及用途。

　　2．熟悉直线相关与回归的统计分析方法及对结论的评价。

　　二、复习思考题

　　[是非题]

　　1．回归系数越大，两变量关系越密切。（ ）

　　2．样本回归系数b＜0，且有显著意义，可认为两变量呈负相关。（ ）

　　3．同一样本的b和r的假设检验结果相同。（ ）

　　4．R=0.08，就可以认为两变量相关非常密切。（ ）

　　5．建立回归方程Y=a+bx，且b有显著意义，就可认为X和y 间存在因果关系。 （ ）

　　6．相关系数的假设检验P值愈小，则说明两变量X与Y间的关系愈密切。（ ）

　　7．当相关系数为0.78，而P＞0.05时，表示两变量X与Y相关密切。（ ）

　　8．有一资料作相关分析，t检验结果为tr=4.24，若作回归分析，tb≥4.24。（）

　　9．根据样本算得一相关系数r，经t检验，P＜0.01，说明r来自高度相关的相关总体。 （）

　　10．Sy.x为各观察值Y距回归直线的标准差。如果变量X与y 的相关系数r=1，则必定sy.x=0。

　　[选择题]

　　1．两组资料中，回归系数b较大的一组。

　　（1）则r也较大；         （2）则r也较小；

　　（3）两变量关系较密切；　 （4）r可能大也可能小。

　　2．同一资料，如将X作自变量，Y作因变量，得回归系数b；将Y作自变量，X作因变量，得回归系数b´，则相关系数r为。

　　（1）bb´　 （2）b+b´/2

　　（3）b+b´    （4）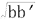

　　3．若r1＞r0.01(n1´),r2＞r_0.05(n₂´)则可认为。

　　（1）第一组资料中两变量相关较密切；

　　（2）第二组资料中两变量相关较密切；

　　（3）很难说那一组资料中两变量相关较密切；

　　（4）至少可以说两组资料中两变量相关密切程度不一样。

　　4．下列哪一式可出现负值；

　　（1）Σ（X-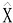）² 　 （2）ΣY²-（ΣY）²/n

　　（3）Σ(Y-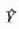)²    （4）Σ(X-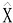)(Y-)

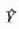　　5.Y=7+2X是1～7儿童以年龄（岁）估计体重（kg）的回归方程，若体重以市斤为单位，则此方程：

　　（1）截距改变     （2）回归系数改变

　　（3）两者都改变 　（4）两者都不改变

　　三、习题

　　某监测站拟用极谱法替代碘量法来测定水中溶解氧含量。今对13个水样同时用两种方法测定，结果如下，求相关系数及回归方程式。