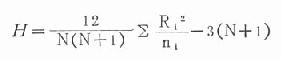仙一网 - 文献资料 - 医学书籍 - 预防医学

第三节　多组资料的比较

　　H检验（Kruskal-Wallis法）是用于完全随机设计的多个样本比较的非参数法。其具体步骤见例21.3。

　　例21.3 某地监测大气中SO2的日均浓度，按不同功能区设置采样点，结果见表21-4“浓度”栏所示，问各功能区SO2日均浓度有无差别？

表21-4 某地1990年1月份SO2日均浓度（μg/m3）

对照区 工业区 商业区 居民区
浓度（1） 秩次（2） 浓度（3） 秩次（4） 浓度（5） 秩次（6） 浓度（7） 秩次（8）
10 1 467 9 231 6 338 7
30 2 665 15 501 11 352 8
30 3 709 18 630 13.5 485 10
40 4 802 19 669 16 511 12
51 5 851 20 677 17 630 13.5
Ri 15 　 81 　 63.5 　 50.5
ni 5 　 5 　 5 　 5

　　(一)建立假设

　　H0：四个功能区SO2日均浓度总体分布相同

　　H1：四个功能区SO2日均浓度总体分布不同或不全相同

　　α=0.05

　　（二）编秩

　　先将各组数据由小到大排列，再将各组数据由小到大统一编秩，不同组的相同数据取其平均秩次。如本例有2个630，分别在第（5）、（7）栏，其平均秩次为（13+14）/2=13.5。

　　（三）求各组秩和（Ri）

　　分别将各组秩次相加得Ri

　　（四）计算统计量H值

　　按式（21.4）计算。式中ni为各组观察值个数，N=Σni

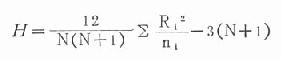　　公式（21.4）

　　本例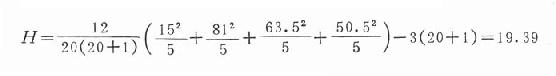

　　（五）确定P值，作出推论

　　若组数K=3，每组例数≤5，可查附表21-3“秩和检验用H界值表”得出P值；若超出附表21-3的范围，可按v=k-1查x2界值表得出P值。本例k=4，超出附表21-3范围，按v=4-1=3查x2界值表，x20.01(3)=11.34,P＜0.01,按α=0.05检验水准拒绝H0，可认为四种功能区SO2日均浓度有差别。

附表21-1 符号秩和检验临界值表

对子数n T0.05 T0.02 T0.01 对子数n T0.05 T0.02 T0.01
6 0 — — 16 29 23 19
7 2 0 — 17 34 27 23
8 3 1 0 18 40 32 27
9 5 3 1 19 46 37 32
10 8 5 3 20 52 43 37
11 10 7 5 21 58 49 42
12 13 9 7 22 65 55 48
13 17 12 9 23 73 62 54
14 21 15 12 24 81 69 61
15 25 19 15 25 89 76 68

附表21-2 等级总和数临界值（双侧检验）

n2较大n P

n1=    较 小  n
2 3 4 5 6 7 8 9 10 11 12 13 14 15
4 0.05 　 　 10 　 　 　 　 　 　 　 　 　 　 　
0.01 　 　 — 　 　 　 　 　 　 　 　 　 　 　
5 0.05 　 6 11 17 　 　 　 　 　 　 　 　 　 　
0.01 　 — — 15 　 　 　 　 　 　 　 　 　 　
6 0.05 　 7 12 18 26 　 　 　 　 　 　 　 　 　
0.01 　 — 10 16 23 　 　 　 　 　 　 　 　 　
7 0.05 　 7 13 20 27 36 　 　 　 　 　 　 　 　
0.01 　 — 10 17 24 32 　 　 　 　 　 　 　 　
8 0.05 3 8 14 21 29 38 49 　 　 　 　 　 　 　
0.01 — — 11 17 25 34 43 　 　 　 　 　 　 　
9 0.05 3 8 15 22 31 40 51 63 　 　 　 　 　 　
0.01 — 6 11 18 26 35 45 56 　 　 　 　 　 　
10 0.05 3 9 15 23 32 42 53 65 78 　 　 　 　 　
0.01 — 6 12 19 27 37 47 58 71 　 　 　 　 　
11 0.05 4 9 16 24 34 44 55 68 81 96 　 　 　 　
0.01 — 6 12 20 28 38 49 61 74 87 　 　 　 　
12 0.05 4 10 17 26 35 46 58 71 85 99 115 　 　 　
0.01 — 7 13 21 30 40 51 63 76 90 106 　 　 　
13 0.05 4 10 18 27 37 48 60 73 88 103 119 137 　 　
0.01 — 7 14 22 31 41 53 65 79 93 109 125 　 　
14 0.05 4 11 19 28 38 50 63 76 91 106 123 141 160 　
0.01 — 7 14 22 32 43 54 67 81 96 112 129 147 　
15 0.05 4 11 20 29 40 52 65 79 94 110 127 145 164 185
0.01 — 8 15 23 33 44 56 70 84 99 115 133 151 171
16 0.05 4 12 21 31 42 54 67 82 97 114 131 150 169 　
0.01 — 8 15 24 34 46 58 72 86 102 119 137 155 　
17 0.05 5 12 21 32 43 56 70 84 100 117 135 154 　 　
0.01 — 8 16 25 36 47 60 74 89 105 122 140 　 　
18 0.05 5 13 22 33 45 58 72 87 103 121 139 　 　 　
0.01 — 8 16 26 37 49 62 76 92 108 125 　 　 　
19 0.05 5 13 23 34 46 60 74 90 107 124 　 　 　 　
0.01 3 9 17 27 38 50 64 78 94 111 　 　 　 　
20 0.05 5 14 24 35 48 62 77 93 110 　 　 　 　 　
0.01 3 9 18 28 39 52 66 81 97 　 　 　 　 　
21 0.05 6 14 25 37 50 64 79 95 　 　 　 　 　 　
0.01 3 9 18 29 40 53 68 83 　 　 　 　 　 　
22 0.05 6 15 26 38 51 66 82 　 　 　 　 　 　 　
0.01 3 10 19 29 42 55 70 　 　 　 　 　 　 　
23 0.05 6 15 27 39 53 68 　 　 　 　 　 　 　 　
0.01 3 10 19 30 43 57 　 　 　 　 　 　 　 　
24 0.05 6 16 28 40 55 　 　 　 　 　 　 　 　 　
0.01 3 10 20 31 44 　 　 　 　 　 　 　 　 　
25 0.05 6 16 28 42 　 　 　 　 　 　 　 　 　 　
0.01 3 11 20 32 　 　 　 　 　 　 　 　 　 　
26 0.05 7 17 29 　 　 　 　 　 　 　 　 　 　 　
0.01 3 11 21 　 　 　 　 　 　 　 　 　 　 　
27 0.05 7 17 　 　 　 　 　 　 　 　 　 　 　 　
0.01 4 11 　 　 　 　 　 　 　 　 　 　 　 　
28 0.05 7 　 　 　 　 　 　 　 　 　 　 　 　 　
0.01 4 　 　 　 　 　 　 　 　 　 　 　 　 　

附表21-3 秩和检验用H界值表

n n1 n2 n3 P
0.05 0.01
7 3 2 2 4.71 　
3 3 1 5.14 　
8 3 3 2 5.36 　
4 2 2 5.33 　
4 3 1 5.21 　
5 2 1 5.00 　
9 3 3 3 5.60 7.20
4 3 2 5.44 6.44
4 4 1 4.97 6.67
5 2 2 5.16 6.53
5 3 1 4.96 　
10 4 3 3 5.73 6.75
4 4 2 5.45 7.04
5 3 2 5.25 6.82
5 4 1 4.99 6.95
11 4 4 3 5.60 7.14
5 3 3 5.65 7.08
5 4 2 5.27 7.12
5 5 1 5.13 7.31
12 4 4 4 5.69 7.65
5 4 3 5.63 7.44
5 5 2 5.34 7.27
13 5 4 4 5.26 7.76
5 5 3 5.71 7.54
14 5 5 4 5.64 7.79
15 5 5 5 5.78 7.98