第十九章 计量数据分析(二)
提要 反映正态分布计量资料抽样误差大小的指—标准误;计量资料的统计推断:总体均数、可信区间的估计和假设检验(u检验,t检验,方差分析);假设检验中的两类错误。
第一节 均数的抽样误差和总体均数的估计
一、均数的抽样误差
第十六章讲了总体与样本的关系。抽样研究的目的是用样本信息推断总体特征。假设要了解某地20岁健康男大学生身高的总体均数,我们在该地随机抽取了110名健康男大学生,得身高的样本均数为172.73(cm),可用它估计该地20岁健康男大学生身高的总体均数。由于存在变异,用样本算得的样本均数x往往不等于总体均数μ;若再从该地20岁健康男大学生中随机抽取含量皆为110人的很多个样本,因各样本包含的个体不同,所得的各个样本均数也不一定都相等,这种由抽样而造成的样本均数与总体均数之差异或各样本均数之差异称为均数的抽样误差。
在抽样研究中,抽样误差是不可避免的,但可以估计其大小,可通过下面的模拟试验说明。现把例18.2中110名20岁健康男大学生的身高写在110个玻璃球上,把该110个身高数值作为假设的有限总体,其总体均数μ=172.73(cm),标准差σ为4.09(cm)。将这些玻璃球放在布袋中作随机抽样试验,每次从中随机抽取10个玻璃球为一样本,记录下数据并计算其均数、标准差、然后把10个玻璃球再放入布袋,充分混匀后再抽,共重复100次,求得100个样本均数x和标准差s,其样本均数入表19-1。
表19-1 100个10球样本均数
| 173.22 | 172.06 | 170.89 | 174.07 | 172.60 | 173.14 | 172.61 | 172.26 | 171.93 | 172.85 |
| 175.23 | 173.76 | 174.77 | 172.57 | 171.76 | 172.74 | 173.36 | 173.69 | 171.10 | 173.40 |
| 173.87 | 172.70 | 173.23 | 173.08 | 172.46 | 171.54 | 171.72 | 170.95 | 172.89 | 173.43 |
| 170.61 | 173.82 | 171.02 | 173.11 | 172.51 | 172.07 | 171.60 | 171.79 | 172.98 | 172.05 |
| 171.11 | 173.66 | 171.21 | 173.15 | 172.12 | 172.53 | 173.21 | 173.25 | 172.03 | 172.42 |
| 175.02 | 171.45 | 173.76 | 176.02 | 173.52 | 172.28 | 170.59 | 171.93 | 173.54 | 172.44 |
| 172.05 | 173.44 | 174.01 | 172.77 | 174.04 | 171.37 | 172.07 | 173.85 | 173.06 | 170.41 |
| 171.88 | 173.38 | 172.83 | 170.89 | 174.55 | 171.45 | 174.11 | 171.88 | 172.78 | 173.73 |
| 171.73 | 172.58 | 174.50 | 172.58 | 172.89 | 173.40 | 174.21 | 172.34 | 171.18 | 171.19 |
| 172.70 | 172.77 | 173.47 | 172.13 | 172.56 | 172.13 | 169.63 | 170.71 | 172.63 | 172.14 |
上述模拟试验的结果表明,在抽样研究中抽样误差是不可避免的。反映均数抽样误差大小的指标是样本均数x的标准差,简称标准误(standard error)。
二、标准误的计算
按照前述标准差的加权计算法,将表19-1的资料归纳成表19-2,可看出样本均数的分布仍服从正态分布,然后按式(18.2),(18.14)计算样本均数的均数(记作x)和样本均数的标准差(记作sx)。
表19-2 100个样本均数的频数表及x、sx计算表
| 身高组段(cm) | 频数f | 组中值f | fX | FX2 |
| 169~ | 1 | 169.5 | 169.5 | 28730.25 |
| 170~ | 7 | 170.5 | 1193.5 | 203491.75 |
| 171~ | 19 | 171.5 | 3258.0 | 558832.75 |
| 172~ | 36 | 172.5 | 6210.0 | 1071225.00 |
| 173~ | 26 | 173.5 | 4511.0 | 782658.50 |
| 174~ | 8 | 174.5 | 1396.0 | 243602.00 |
| 175~ | 2 | 175.5 | 351.0 | 61600.50 |
| 176~177 | 1 | 176.5 | 176.5 | 31152.25 |
| 合计 | 100 | 17266.0 | 2981293.00 |
数学上可以证明:①各样本均数的均数x等于μ;②标准误σx(理论值)按式(19.1)计算
σx=σ/x公式(19.1)
式中,σ为总体标准差,n为样本含量。
本试验各样本试验均数的均数x=172.66(cm)与μ=172.73(cm)相近,按式(19.1)算得的σx=4.09/x=1.29(cm)与本试验所得的样本均数的标准差sx=1.21(cm)也很接近。
在实际的抽样研究中,σ常属未知,通常用单一样本标准差s来估计,得出标准误sx(估计值),其计算公式为:
sx=s/x 公式(19.2)
例如模拟试验中1号样本的标准差s=4.05(cm),其标准误sx(估计值)=4.05/x=1.28(cm)。
标准误sx用来说明抽样误差的大小。由式(19.1)、(19.2)可知,标准误的大小与标准差的大小成正比,与x成反比。
三、t分布(t-distribution)
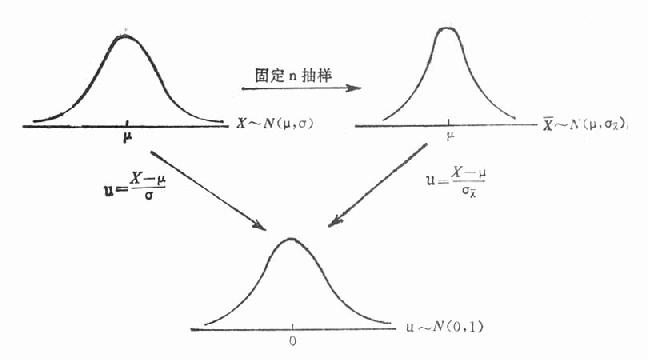
在前一章正态分布中曾提到,为了应用方便,常将正态变量进行变量变换-u变换[u=(X-μ)/σ],使一般的正态分布变换为标准正态分布。上述抽样模拟试验表明,在正态分布总体中以固定n(本试验n=10)抽取若干样本时,样本均数x的分布仍服从正态分布,即N(μ,σx)。那末,对此进行u变换[u=(x-μ)/σx],也可变换为标准正态分布N(0,1),如图19-1。

图19-1 标准正态分布示意图
由于实际工作中,σ往往是未知的,常用sx作为σx的估计值,为与u变换区别,称为t变换[t=(x-μ)/sx],t值的分布为t分布。t分布的特征:①是以0为中心的对称分布的曲线;②其形态变化与n(确切地说与自由度v)大小有关。自由度v越大,t分布越接近u分布;自由度越小,t 分布中间越低平且两端向外伸展,所以t分布不是一条曲线,而是一簇曲线,如图19-2。因此,t曲线下面积为95%或99%的界值不是一个常量,而是随自由度大小而变化的。为了便于应用,统计学上根据自由度大小与t曲线下面积的关系,换算出t值表(附表19-1)以备参考。因t分布是以0为中心的对称分布,故附表19-1只列出正值,若算得的t值为负值时,可用其绝对值查表。
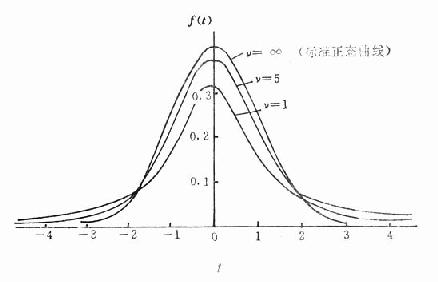
图19-2 自由度分别为1、5、∞的t分布
四、总体均数可信区间(confidence interval)的估计
用样本指标(统计量,statistic)来估计总体指标(参数,parameter),称为参数估计。是抽样研究的主要目的之一。参数估计的方法有两种。一是点(值)估计(point estimation),如用样本均数估计总体均数。该法简单,但未考虑抽样误差,而抽样误差在抽样研究中又是不可避免的;二是用区间估计(interval estimation),即按一定的可信度估计未知总体均数所在范围。统计上习惯用95%(或99%)可信区间表示总体均数μ有95%(或99%)的可能在某一范围。下面以总体均数μ的95%可信区间为例,介绍其计算公式。σ已知时按正态分布原理计算,σ未知时按t分布原理计算。
(一)σ已知时:由u分布可知,正态曲线下有95%的u值在±1.96之间,即:
-1.96≤u≤+1.96
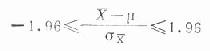
移项后,x-1.96σx≤μ≤x+1.96σx,故总体均数μ的95%可信区间为
(x-1.96σx,x+1.96σx) 公式(19.3)
(二)σ未知,但n足够大(如n>100)时:由t分布可知,当自由度v越大,t分布越逼近u分布,此时t曲线下有95%的t值约在±1.96之间,即
-1.96≤t≤+1.96
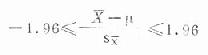
x-1.96σx≤μ≤x+1.96σx,故总体均数μ的95%可是信区间为
(x-1.96sx,x+1.96sx)公式(19.4)
(三)σ未知且n小时:某自由度v的t曲线下有95%的t值在±t0.05(v)之间,即
-t0.05(v)≤t≤t0.05(v)
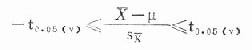
x-t0.05(v)sx≤μ≤x+t0.05(v)sx,故总体均数μ的95%可信区间为
(x-t0.05(v)sx,x+t0.05(v)sx)公式(19.5)
例19.1 由例18.2某地110名20岁健康男大学生的身高资料,算得身高均数x为172.73(cm),标准差为4.09(cm),试估计该地20岁健康男大学生身高均数的95%可信区间。
该例n=110,n较大,按式(19.4)计算
(172.73-1.96×4.09/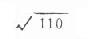 ,172.3+1.96×4.09/
,172.3+1.96×4.09/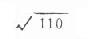 )=(171.79,173.49)该地20岁健康男大学生身高均数的95%的可信区间为171.97~173.49(cm)。
)=(171.79,173.49)该地20岁健康男大学生身高均数的95%的可信区间为171.97~173.49(cm)。
例19.2 由例18.1的11名20岁健康男大学生身高资料得出x为172.25(cm),s为3.31(cm),试估计该地20岁健康男大学生身高均数的95%可信区间。
该例n=11,n较小,按式(19.5)计算。V=11-1=10,由t值表查得t0.05(10)=2.228。
(172.25-2.228×3.31/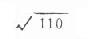 ,172.25+2.228×3.31/
,172.25+2.228×3.31/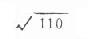 )=(170.03,174.47)该地20岁健康男大学生身高均数的95%可信区间为170.03~174.47(cm)。
)=(170.03,174.47)该地20岁健康男大学生身高均数的95%可信区间为170.03~174.47(cm)。