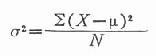
第二节 离散趋势指标
计量资料的频数分布有集中趋势和离散趋势两个主要特征，只有把两者结合起来，才能全面地认识事物，通过例18.8可进一步说明这一问题。
例18.8 有3组同龄男孩体重（kg）如下，其平均体重x都是30（kg），试分析其离散趋势。
| 甲组 | 26 | 28 | 30 | 32 | 34 |
| 乙组 | 24 | 27 | 30 | 33 | 36 |
| 丙组 | 26 | 29 | 30 | 31 | 34 |
虽然三组资料的均数相等，即集中趋势相同，但各组内数据参差不齐的程度（变异度）不同，也就是说三组的离散趋势不同。
描述一组同质计量资料离散趋势的常用指标有全、四分位数间距方差和标准差，其中方差和标准差最常用。
一、全距（range）
亦称极差，用R表示。全距是一组观察值中最大值与最小值之差，用于反映个体变异范围的大小。全距大，说明变异度大；反之，说明变异度小。如例18.8中乙组全距为12(kg)，比甲、丙两组8（kg）大，表明乙组变异度大。全距适用于任何分布的计量资料（末端无确切数值者除外）。
用全距来表达变异度的大小，简单明了，故曾广为使用。但它不能反映组内所有数据的变异度，如上述甲、丙两组变异度的差异就反映不出来；其更大的缺点是易受个别特大或特小数值的影响，往往样本越大，全距亦会越大。
二、四分位数间距（quartile interval）
四分位数间距是上四分位数Qu（即P75）与下四位数QL（即P25）之差，其间包括了全部观察值的一半，用Q表示。它和极差类似，数值越大，说明变异越大；反之，说明变异越小。四分位数间距比极差稳定，但仍未考虑到每个观察值的变异度。它适用于偏态分布资料，特别是分布末端无确定数据不能计算全距、方差和标准差的资料。
例18.9 求表18-4中数据的四分位数间距。
QL=P25=12+12/58（164×25%-25）=15.3(小时)
Qu=P75=24+12/40 (164×75%-83)=36.0(小时)
Q=Qu-QL=P75-P25=20.7（小时）
三、方差（variance）和标准差（standard deviation）
为了克服极差的缺点，需全面地考虑组内每个观察值的离散情况。因为组内每一观察值（亦称变量值）与总体均数的距离大小都会影响总体的变异度，故有人提出以各变量值离均差（X-μ）的平方和除以变量值的总个数N，来反映变异度大小，称为总体方差，用σ2示之。
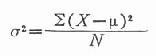
公式(18.10)
由式可见，各个离均差平方后，原来的度量单位变成了平方单位。为了用原单位表示而将总体方差开方，称为总体标准差。
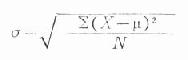
公式（18.11）
以上是总体方差和标准差。实际工作中经常得到的是样本资料，μ是未知的，只能用样本均数x来代替μ，用样本含量n代替N，按公式（18.11）算得的标准差常比σ小，美国统计学家W.S.Gosset提出用n-1代替n，求得样本标准差s，即
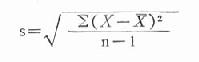
公式（18.12）
式中的n-1，在统计学上称为自由度（degree of freedom）
数学上可以证明离均差平方和Σ（X-x）2=ΣX2-（ΣX）2/n，故公式（18.2）可演变为：
直接法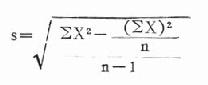 
公式（18.13）
加权法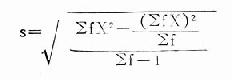 
公式（18.14）
方差与标准差适用于对称分布，特别是正态或近似正态分布资料。
例18.10 试分别计算例18.8中三组男孩体重资料的标准差。
甲组：n=5，ΣX=26=28+30+32+34=150
ΣX2=262+282+302+322+342=4540
按式（18.13）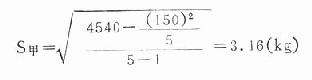
乙组：n=5，ΣX=150，ΣX2=4590
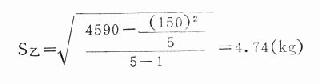
丙组：n=5,ΣX=150,ΣX2=4534
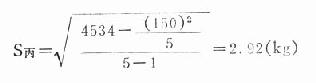
以上计算表明：S丙＜S甲＜S乙亦即乙组的变量度最大，甲组次之，丙组最小。
例18.11 求表18-2中110名20岁健康男大学生身高的标准差。
由表18-2，已知Σf=110，ΣfX=19000，再用第（2）栏乘第（4）栏后相加得ΣfX2。如本例，ΣfX2=163×163+165×660+……+183×366=3283646代入式（18.14）
四、标准差的应用
（一）表示观察值的变异程度（或离散程度）
1．在两组（或几组）资料均数相近、度量单位相同的条件下，标准差大，表示观察值的变异度大，即各观察值离均数较远，均数的代表性较差；反之，表示各观察值多集中在均数周围，均数的代表性较好。
2．若比较度量单位不同或均数相差悬殊的两组（或几组）观察值的变异度时，需计算变异系数（coefficient of variation用CV表示）进行比较，其计算公式为：
CV= s/x×100% 公式（18.15） 公式(18.15)
式中s为样本标准差，x为样本均数。
例18.12 某地调查20岁男大学生110名，其身高均数为172.73(cm),标准差为4.09(cm)；其体重均数为55.04(kg)，标准差为4.10(kg)，欲比较两者变异度何者为大，宜先计算变异系数再比较。
身高 CV=4.09/172.73×100%=2.37%
体重 CV=4.10/55.04×100%=7.45%
由此可见，该地20名男大学生体重的变异度大于身高的变异度，说明身高这个指标比较稳定。
（二）结合均数描述正态分布的特征和估计医学正常值范围，详见第三节。
（三）结合样本含量n计算标准误，详见第十九章。