
第九章 直线相关与回归
前面各章介绍的统计方法都只涉及单一变量,即或进行两组或多组比较,所比较的仍然是同一变量,而且是以讨论各组间该变量的相差是否显著为中心环节。但医学领域里常可在一个统一体中遇到两个或多个变量之间存在着相互联系、相互制约的情况,如同一批水样的浊度与透光率,同一批人的年龄与血压以及身长、体重与胸围等。因而研究问题的方法就需要扩展。在统计方法中通常是用相关与回归的方法来研究不同变量之间的这种相互依存和互为消长的关系。相关与回归的种类较多,本章所涉及的只是其中最简单的直线相关与直线回归,简称相关与回归。
相关与回归即有区别又有联系,表达事物或现象间的在数量方面相互关系的密切程度用相关系数;说明一变量依另一变量的消长而变动的规律用回归方程。现先介绍相关,再介绍回归。
第一节 直线相关
一、相关系数的意义
相关分析是用相关系数(r)来表示两个变量间相互的直线关系,并判断其密切程度的统计方法。相关系数r没有单位。在-1~+1范围内变动,其绝对值愈接近1,两个变量间的直线相关愈密切,愈接近0,相关愈不密切。相关系数若为正,说明一变量随另一变量增减而增减,方向相同;若为负,表示一变量增加、另一变量减少,即方向相反,但它不能表达直线以外(如各种曲线)的关系。
为判断两事物数量间有无相关,可先将两组变量中一对对数值在普通方格纸上作散点图,如图9.1~9.8所示。图中点子的分布可出现以下几种情况:
正相关——见图9.1,各点分布呈椭圆形,Y随X的增加而增加,X亦随Y的增加而增加,此时1>r>0。椭圆范围内各点的排列愈接近其长轴,相关愈密切,当所有点子都在长轴上时,r=1(见图9.2),称为完全正相关。
负相关——见图9.3,各点分布亦呈椭圆形,Y随X的增加而减少,X也随Y的增加而减少,此时0>r>-1。各点排列愈接近其长轴,相关愈密切,当所有点子都在长轴上时,r=1(见图9.4),称为完全负相关。
在生物现象中,完全正相关或完全负相关甚为少见。
无相关——见图9.5、图9.6和图9.7,X不论增加或减少,Y的大小不受其影响;反之亦然。此时r=0。另外,须注意有时虽然各点密集于一条直线,但该直线与X轴或Y轴平行,即X与Y的消长互不影响,这种情况仍为无相关。
非线性相关——见图9.8,图中各点的排列不呈直线趋势,却呈某种曲线形状,此时r≈0,类似这种情况称为非线性相关。

图9.1—9.8 不同相关系数的散点示意图
二、相关系数的计算及假设检验
(一)相关系数计算法
计算相关系数的基本公式为:
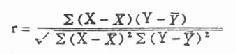 (9.1)
(9.1)
式(9.1)中r为相关系数,∑(X-X)2为X的离均差平方和,∑(Y-Y)2为Y的离均差平方和,∑(X-X)(Y-Y)为X与Y的离均差乘积之和,简称离均差积之和,此值可正可负。以此式为基础计算相关系数的方法称积差法,在实际应用时式(9.1)中各离均差平方和(简称差方和)与积之和可化为
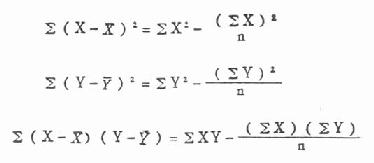
(9.2)
现举例说明计算相关系数的一般步骤:
例9.1 测定15名健康成人血液的一般凝血酶浓度(单位/毫升)及血液的凝固时间(秒),测定结果记录于表9.1第(2)、(3)栏,问血凝时间与凝血酶浓度间有无相关?
1.绘图,将表9.1第(2)、(3)栏各对数据绘成散点图,见图9.9。
2.求出∑X、∑Y、∑X2、∑Y2、∑XY,见表9.1下方。
3,代入公式,求出r值。
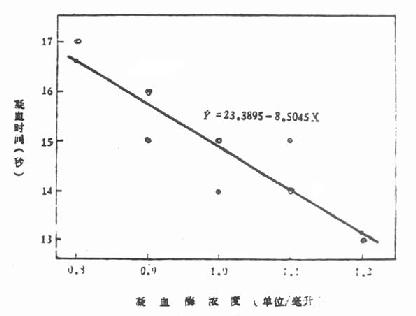
图9.9 凝血时间与凝血酶浓度散点图及回归直线
表9.1 相关系数计算表
| 受试者号
(1) |
凝血酶浓度(单位/毫升) X (2) |
凝血时间(秒) Y (3) |
| 1 | 1.1 | 14 |
| 2 | 1.2 | 13 |
| 3 | 1.0 | 15 |
| 4 | 0.9 | 15 |
| 5 | 1.2 | 13 |
| 6 | 1.1 | 14 |
| 7 | 0.9 | 16 |
| 8 | 0.9 | 15 |
| 9 | 1.0 | 14 |
| 10 | 0.9 | 16 |
| 11 | 1.1 | 15 |
| 12 | 0.9 | 16 |
| 13 | 1.1 | 14 |
| 14 | 1.0 | 15 |
| 15 | 0.8 | 17 |
| 合计 | 15.1 | 222 |
∑X=15.1 ∑Y=222
∑XY=221.7
∑X2=15.41∑Y2=3304 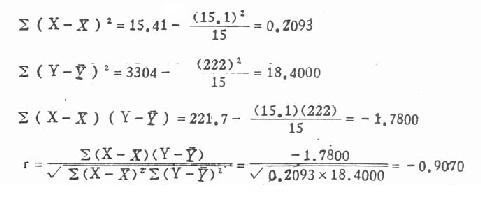
本例的相关系数r=-0.9070,负值表示血凝时间随凝血酶浓度的增高而缩短;绝对值∣-0.9070∣表示这一关系的密切程度。至于此相关系数是否显著,则要经过下面的分析。
(二)相关系数的假设检验
虽然样本相关系数r可作为总体相关系数ρ的估计值,但从相关系数ρ=0的总体中抽出的样本,计算其相关系数r,因为有抽样误差,故不一定是0,要判断不等于0的r值是来自ρ=0的总体还是来自ρ≠0的总体,必须进行显著性检验。检验假设是ρ=0,r与0的差别是否显著要按该样本来自ρ=0的总体概率而定。如果从相关系数ρ=0的总体中取得某r值的概率P>0.05,我们就接受假设,认为此r值的很可能是从此总体中取得的。因此判断两变量间无显著关系;如果取得r值的概率P≤0.05或P≤0.01,我们就在α=0.05或α=0.01水准上拒绝检验假设,认为该r值不是来自ρ=0的总体,而是来自ρ≠0的另一个总体,因此就判断两变量间有显著关系。
由于来自ρ-0的总体的所有样本相关系数呈对称分布,故r的显著性可用t检验来进行。本例r=-0.9070,进行t检验的步骤为:
1.建立检验假设,H0:ρ=0,H1:ρ≠0,α=0.01
2.计算相关系数的r的t值:
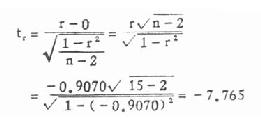 (9.3)
(9.3)
3.查t值表作结论
ν=n-2=15-2=13
根据专业知识知道凝血酶浓度与凝血时间之间不会呈正相关,故宜用单侧界限,查t值表得
t0.01,13=2.650
今∣tr∣>t0.01,13,P<0.01,在α=0.01水准上拒绝H0,接受H1,故可认为凝血时间的长短与血液中酶浓度有负相关。
为简化tr检验的计算过程,数理统计工作者根据t分配表,已把不同自由度时r的临界值求出,并列成相关系数界值表(见附表11)。故求相关系数后,只需查表就可知道该r值是否显著,而不必再计算tr值。
r的显著性界限为
|r|
r0.05,,≤|r|<r0.01,, 0.05≥P>0.01
在α=0.05水准上相关显著
|r|≥r0.01,, P≤0.01 在α=0.01水准上相关显著
例9.1的ν =15-2=13,查附表11中P(1)的界值,得:
r0.05,13=0.441r0.01,13=0.592
现r=-0.9070,∣r∣>r0.01,13,P<0.01,按α=0.01水准,拒绝HO,接受H1。认为ρ≠0,说明凝血时间的长短与血液中凝血酶浓度有负相关。结论与计算所得一致。
相关系数的显著性与自由度的大小有关,如n=3,ν=1时,虽r=-0.9070,却为不显著;若ν=400时,即使r=0.1000,亦为显著。因此不能只看r的值,不考虑ν就下结论。