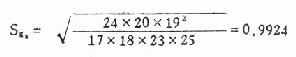
第三节 正态性检验与两方差的齐性检验
检验两个样本均数相差的显著性时,我们先有假定:第一个样本系从均数为μ1、方差为σ12的正态总体中随机取出,第二个样本取自另一个类似的总体,相应的总体参数为μ2与σ22,两个总体的方差应相等即σ12=σ22,然后才可用上述方法进行显著性检验,如果资料呈显著偏态,或两组方差相差悬殊,就要考虑用第十章非参数统计方法处理,或者通过变量代换,使上述条件得到满足。那么,怎样知道手头的样本资料是否服从正态分布及两组方差是否相差显著呢?要对手头资料作正态检验及方差齐性检验。下面分别用实例介绍常用的正态性检验和两方差齐性检验的方法。
一、正态性检验
有些统计方法只适用于正态分布或近似正态分布资料,如用均数和标准差描述资料的集中或离散情况,用正态分布法确定正常值范围及用t检验两均数间相差是否显著等,因此在用这些方法前,需考虑进行正态性检验。
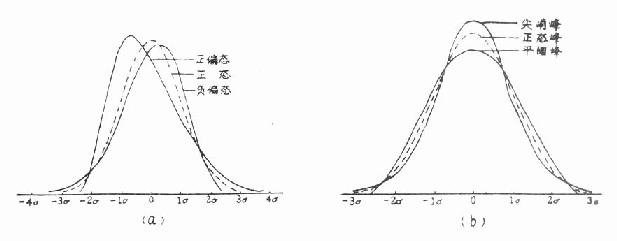
正态分布的特征是对称和正态峰。分布对称时众数和均数密合,若均数-众数>0,称正偏态。因为有少数变量值很大,使曲线右侧尾部拖得很长,故又称右偏态;若均数-众数<0称负偏态。因为有少数变量值很小,使曲线左侧尾部拖得很长,故又称左偏态,见图7.1(a)。
正态曲线的峰度叫正态峰,见图7.1(b)中的虚线,离均数近的或很远的变量值都较正态峰的多的称尖峭峰,离均数近或很远变量值都较正态峰的少的称平阔峰。

图7.1 频数分布的偏度和峰度
正态性检验的方法有两类。一类对偏度、峰度只用一个指标综合检验,另一类是对两者各用一个指标检验,前者有W法、D法、正态概率纸法等,后者有动差法亦称矩法。现仅将W法与动差法分述于下;
1.W法 此法宜用于小样本资料的正态性检验,尤其是n≤50时,检验步骤如下;
(1)将n个变量值Xi从小至大排队编秩。
X1 见表7.5第(1)栏,表中第(2)、第(3)栏是变量值,第(2)栏由上而下从小至大排列,第(3)栏由下而上从小至大排列。第(4)栏是第(3)栏与第(2)栏之差。 (2)由附表5按n查出ain系数列入表7.5第(5)栏,由于当n为奇数时,对应于中位数秩次的ain为0,所以中位数只列出,不参加计算。第(6)栏是第(5)栏与第(4)栏的乘积。 (3)按式(7.8)计算W值 式中分子的∑,当n是偶数时,为 第(6)栏的合计平方后即为分子。分母按原始资料计算。 (4)查附表6得P值,作出推断结论,按n查得W(n,α),α是检验前指定的检验水准,若W>W(n,α)则在α水准上按受H0,资料来自正态分布总体,或服从正态分布;若W≤W(n,α),则在α水准上拒绝H0,接受H1,资料非正态。 例7.8 测得20例40—49岁健康人右侧腓总神经的传导速度(m/sec)如表7.5第(2)、第(3)栏,试检验此资料是否服从正态分布。 H0:总体服从正态分布 H1:总体为非正态分布 α=0.05 计算表7.5各栏。 表7.5 W法正态性检验计算表 18.2240 ∑ain(Xa-i+1-Xi) ∑Xi=1004 ∑Xi2=50756.16 ∑(X-x )2=355.36 代入式(7.8) W=(18.2240)2/355.36=0.9347 查附表6,n=20,α=0.05,W(20,0.05)=0.905 W>W(20,0.05) P>0.1,在α=0.05水准上接受H0,该资料服从正态分布。 2.动差法 又称矩法。既能用于小样本资料,亦可用于大样本资料的正态性检验。本法运用数学上三级动差和四组动差分别组成偏度系数与峰度系数,然后检验资料中否服从正态分布。当频数分布为正态时,偏度系数与峰度系数分别等于0,但从正态分布总体中抽出的随机样本,由于存在抽样误差,其样本偏度系数g1与样本峰度系数g2不一定为0,为此,需检验g1、g2与0的相差是否有显著性。其检验假设为①偏度系数等于O,即频数分布对称;②峰度系数等于0,即为正态峰。 偏度系数g1、峰度系数g2的公式见式(7.9)与(7.11)。当用频数表资料计算时可用式(7.10)与式(7.12),式中n为例数,f为频数。 g1、g2的抽样误差分别为Sg1与Sg2,见式(7.13)与式(7.14) 假设检验用u检验,其公式为 u1=g1/Sg1 (7.15) u2=g2/Sg2 (7.16) u的显著性界限为 ∣u∣<1.96P>0.05在α=0.05的水准上接受H0。 1.96≤∣u∣<2.580.05≥P>0.01在α=0.05的水准上拒绝H0。 ∣u∣≥2.58P≤0.01在α=0.01的水准上拒绝H0。 例7.9 用动差法检验例7.8的资料是否服从正态分布。 1.H0:频数分布对称,H1:频数分布不对称。 2.H0:频数分布为正态峰,H1:频数分布不是正态峰。 α=0.05 ∑(X-x )2=355.36,∑(X-x )3=-1032.45 ∑(X-x )4=20150.4316 n=20 u2=0.6221/0.9924=0.627 P>0.20 在α=0.05的水准上接受H0,频数分布对称(P>0.05),并为正态峰(P>0.20)。因此可认为该资料服从正态分布。 二、两方差的齐性检验 方差齐性检验的方法是以两方差中较大的方差为分子,较小的方差为分母求一比值(称为F值),然后将求得的F值与临界值比较,看相差是否显著,现举一例说明。 例7.10 某单位测定了蓄电池厂工人32号,得尿氨基乙酰丙酸(mg/l)的平均含量为7.06,方差为42.3072,又测定了化工厂工人6名,得平均含量为3.48,方差为0.9047,试比较两方差的相差是否有显著意义? 检验假设H0:σ12=σ22,H1:σ12≠σ22α=0.05 定方差较大的一组为第1组,较小者为第2组,求出F值,公式为 F=S12/S22,S1>S2 (公式7.17) 本例F=42.3072/0.9047=46.76 现将F值与附表7中的F.05(ν1,ν2)比较。该表上端数值是较大均方(即方差)的自由度,用v1表示,左侧的数值是较小均方的自由度,用ν2表示。本例ν1=n1-1=32-1=31(表内ν1纵行没有31,可查邻近的数值30),ν2=n2-1=6-1=5,查得F.05(30,5)=6.23,本例F=46.76>F.05(30,5),P<0.05,故在α=0.05水准处拒绝H0,接受H1。两方差的差别显著。 (俞元春胡琳 编)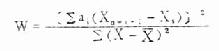 (7.8)
(7.8) 的缩写,当n是奇数时为
的缩写,当n是奇数时为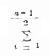 的缩写,表7.5
的缩写,表7.5
秩号
传导速度(m/sec)
i
(1)Xi
(2)Xa-i+1
(3)Xa-i+1-Xi
(4)=(3)-(2)ain
(5)ain(Xa-i+1-Xi)
(6)=(5)(4)
1
40.7
56.7
16.0
0.4734
7.5744
2
40.9
56.0
15.1
0.3211
4.8486
3
46.0
55.0
9.0
0.2565
2.3085
4
47.6
54.9
7.3
0.2085
1.5221
5
47.7
53.5
5.8
0.1686
0.9779
6
48.3
52.9
4.6
0.1334
0.6136
7
49.1
51.8
2.7
0.1013
0.2735
8
50.0
50.9
0.9
0.0711
0.0640
9
50.1
50.9
0.8
0.0422
0.0338
10
50.2
50.8
0.6
0.0140
0.0084
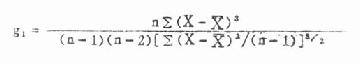
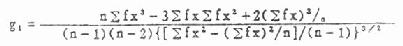 (7.10)
(7.10)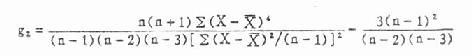 (7.11)
(7.11)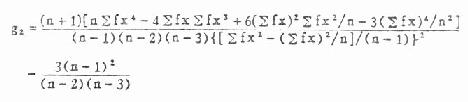 (7.12)
(7.12) (7.13)
(7.13)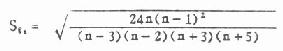 (7.14)
(7.14)