第六章 标准误与可信区间
第一节 抽样误差与标准误
一、抽样误差的意义
在第一章第二节曾提到过样本与总体以及抽样误差的概念,那里谈到,由于存在人与人之间的个体差异,即使从同一总体用同样方法随机抽取例数相同的一些样本,各样本算得的某种指标,如平均数(或率),通常也参差不齐存在一定的差异。样本指标与相应的总体指标之间有或多或少的相差,这一点是不难理解的。如某医生从某地抽了120名12岁男孩,测量其身高,计算出均数为143.10cm,若再从该地抽120名12岁男孩,其平均身高未必仍等于143.10cm,也不一定恰好等于某市12岁男孩身高的总体均数,这种差异,即由于抽样而带来的样本与总体间的误差,统计上叫抽样波动或抽样误差。
抽样误差和系统误差不一样,关系系统误差,当人们一旦发现它之后,是可能找到产生原因而采取一定措施加以纠正的,抽样误差则无法避免。因为客观上既然存在个体差异,那么刚巧这一样本中多抽到几例数值大些的,所求样本均数就会稍大,另一样本多抽到几例数值小些,该样本均数就会稍小,这是不言而喻的。
抽样误差既是样本指标与总体指标之间的误差,那么抽样误差小就表示从样本算得的平均数或率与总体的较接近,有样本代表总体说明其特征的可靠性亦大。但是,通常总体均数或总体率我们并不知道,所以抽样误差的数量大小,不能直观地加以说明,只能通过抽样实验来了解抽样误差的规律性。
二、标准误及其计算
为了表示个体差异的大小,或者说表示某一变量变异程度的大小,可计算标准差等变异指标来说明,现在我们要表示抽样误差的大小,如要问,从同一总体抽取类似的许多样本,各样本均数(或各率)之间的变异程度如何?也可用变异指标来说明。这种指标是:
(一)均数的标准误 为了表示均数的抽样误差大小如何,用的一种指标称为均数的标准误。我们以样本均数为变量,求出它们的标准差即可表示其变异程度,所以将样本均数这“标准差”定名为均数的标准误,简称标准误,以区别于通常所说的标准差。标准差表示个体值的散布情形,而标准误则说明样本均数的参差情况,两者不能混淆。下面用抽样实验进一步说明之。
将100名正常人的红细胞数(万/mm3)写在100颗大小均匀的豌豆上。这些红细胞数见表6.1,其均数为500,标准差为43。把这些豌豆放在一个口袋里,彻底混匀后取出一颗,记下红细胞数,放回袋内,混匀后再取出一颗,记下数字后再放回去,如此继续下去,这是一个取不完的总体,这样每取10个数字作为一个样本,共抽取了一百个样本,并计算每一样本的均数与标准差,例见表6.2。
表6.1 红细胞数抽样实验用的正态总体
μ=500 σ=43(单位:万/立方厘米)
| 383 | 410 | 422 | 429 | 430 | 431 | 435 | 442 | 442 | 444 |
| 445 | 449 | 450 | 452 | 455 | 456 | 459 | 461 | 462 | 463 |
| 465 | 466 | 468 | 469 | 470 | 471 | 472 | 473 | 476 | 477 |
| 478 | 479 | 480 | 481 | 482 | 484 | 485 | 486 | 487 | 488 |
| 489 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 |
| 500 | 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 |
| 511 | 512 | 513 | 514 | 515 | 516 | 518 | 519 | 520 | 521 |
| 522 | 523 | 524 | 527 | 528 | 529 | 530 | 531 | 532 | 534 |
| 535 | 537 | 538 | 539 | 541 | 544 | 545 | 548 | 550 | 551 |
| 555 | 556 | 558 | 565 | 569 | 578 | 590 | 599 | 600 | 617 |
表6.2 红细胞数抽样实验中的样本举例
| 样本号 | 红细胞数(万/立方毫米),X | X | S | |||||||||
| 1 | 383 | 599 | 534 | 442 | 435 | 486 | 478 | 476 | 509 | 544 | 488.6 | 61.65 |
| 2 | 503 | 506 | 520 | 503 | 489 | 410 | 528 | 488 | 509 | 527 | 498.3 | 33.97 |
| 3 | 478 | 463 | 617 | 544 | 498 | 485 | 496 | 462 | 482 | 569 | 509.4 | 50.96 |
| 4 | 529 | 465 | 535 | 473 | 531 | 532 | 556 | 521 | 459 | 383 | 498.4 | 52.63 |
| 5 | 442 | 493 | 462 | 527 | 520 | 519 | 521 | 512 | 482 | 471 | 494.9 | 29.51 |
| ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ |
第一号样本均数与标准差的计算:
X=4.886/10=488.6
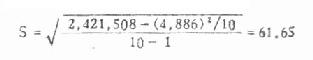
将一百个样本均数加总,得到的数值为50,096.7,又这一百个样本均数平方之和为25,114,830.91,于是代入标准差的计算公式,求得一百个样本均数的标准差又称标准误为
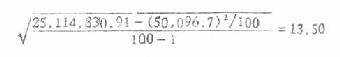
当总体标准差已知时,可计算理论的标准误σχ,公式是
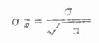 (6.1)
(6.1)
表6.1抽样实验用的总体标准差是43,每个样本的例数是10,代入公式得
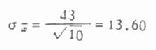
可见由一百个样本均数求得的标准误13.50与理论的标准误13.60比较接近。
在实际工作中,总体标准差往往并不知道,也不象抽样实验那样从同一总体随机抽取n相等的许多样本,而是只有手头一个样本。在此情况下,只能以样本标准差S作为总体标准差σ的估计值。这样,公式6.1中的σ就要用S代替,σχ改为Sχ,以资区别。
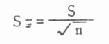 (6.2)
(6.2)
将第1号样本的标准差及例数代入式6.2,得

再若将第2号样本的数字代入,Sχ将成为10.74,余类推。由于不同样本的标准差并不相等,可见Sχ也有抽样波动,这一点是值得注意的,但它仍不失为σχ的较好估计值。
以上介绍了求标准误的三种方法,其实我们平常用的只是式6.2,而通过前两种方法的对比则可使我们明瞭标准误的含义。标准误是描述样本均数变异情况的一个指标,它的大小与总体标准差σ(一般只能用S估计)成正比,而与样本含量n的平方根成反比,因此若标准差小或样本含量大时,求出的标准误就小(标准误小表示样本均数与总体均数较接近),X代表μ较可靠,所以假若手头资料中观察值的变异程度较大(S大)时,为了保
证样本代表总体比较可靠,就得适当增大样本含量(n)。
(二)率的标准误 若总体包括某事件的发生数与未发生数两类,所化成的比例或成数即为总体发生率(符号π)与未发生率(1-π)。从总体中随机抽取许多样本(n相等),算出各个样本率(用P表示),会是或大或小有波动的。为了表示样本率之间或样本率与总体率之间的差异程度,当总体率π已知时,可计算理论的标误σp,其公式是
 (6.3)
(6.3)
实际工作中往往不知道总体率π这时只能以样本率P作为总体率π的估计值,求得率的标准误,并用SP表示,计算公式为
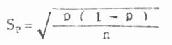 (6.4)
(6.4)
现举例说明其求法。
例6.1 某医生检测了110名成年健康人的尿紫质,发现阳性者11人,阴性者99人,于是算得阳性率P及率的标准误SP如下:
P=11/110×100%=10% (用小数表示为0.10)
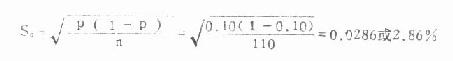
若要进一步增强样本率估计总体率的可靠性,可加大样本含量。
三、样本均数的分布
从同一总体里随机抽取n相同的许多样本,这些样本均数吴正态分布。如前面所述正常人红细胞数的抽样实验中已求得100个样本均数,其中多数与总体均数μ比较接近而集中分布在其周围,且左右基本对称,见表6.3(此表由表6.4中的100个均数划记归组而得)。
表6.3 红细胞抽样实验中100个样本均数的分布
| 组 段 | 460- | 470- | 480- | 490- | 500- | 510- | 520- | 530- | 540- | 合计 |
| 样本数 | 1 | 3 | 18 | 28 | 28 | 13 | 7 | 1 | 1 | 100 |
表6.4 一百个样本的均数、标准差、95%可信区间
| 样本号 | 均数 | 标准差 | 95%可信区间 | 样本号 | 均数 | 标准差 | 95%可信区间 | ||
| 1 | 488.6 | 61.65 | 444.49~532.71 | 2 | 498.3 | 33.97 | 474.01~522.59 | ||
| 3 | 509.4 | 50.96 | 472.96~545.84 | 4 | 498.4 | 52.63 | 460.76~536.04 | ||
| 5 | 494.9 | 29.51 | 473.80~516.00 | 6 | °546.7 | 43.23 | 515.78~577.62* | ||
| 7 | 524.5 | 33.60 | 500.45~548.55* | 8 | 488.3 | 41.04 | 458.94~517.66 | ||
| 9 | 485.3 | 55.14 | 445.85~524.75 | 10 | 502.6 | 48.55 | 467.88~537.32 | ||
| 11 | 495.1 | 40.63 | 466.03~524.17 | 12 | 524.7 | 37.81 | 497.65~551.75 | ||
| 13 | 512.7 | 53.18 | 474.65~550.75 | 14 | 494.8 | 37.24 | 468.15~521.45 | ||
| 15 | 493.6 | 39.94 | 465.03~522.17 | 16 | 495.3 | 29.47 | 474.22~516.38 | ||
| 17 | 491.0 | 19.32 | 477.18~504.82 | 18 | 506.5 | 53.83 | 468.00~545.00 | ||
| 19 | 487.5 | 39.39 | 461.32~517.68 | 20 | 495.9 | 32.70 | 472.51~519.29 | ||
| 21 | 504.8 | 34.76 | 479.94~529.66 | 22 | 512.2 | 44.76 | 483.17~547.23 | ||
| 23 | 496.5 | 40.65 | 467.41~525.59 | 24 | 499.8 | 37.04 | 473.31~526.29 | ||
| 25 | 505.7 | 37.21 | 479.08~532.32 | 26 | 487.7 | 34.50 | 463.02~512.38 | ||
| 27 | 501.5 | 37.35 | 474.79~528.21 | 28 | 476.1 | 29.64 | 454.91~497.29* | ||
| 29 | 523.2 | 51.57 | 486.31~560.09 | 30 | 509.5 | 33.61 | 485.45~533.55 | ||
| 31 | 494.2 | 28.60 | 473.75~514.65 | 32 | 506.2 | 25.29 | 483.10~524.30 | ||
| 33 | 501.1 | 27.88 | 481.15~521.05 | 34 | 520.6 | 30.23 | 498.98~542.22 | ||
| 35 | 492.0 | 42.18 | 461.82~522.18 | 36 | 509.6 | 19.17 | 495.89~523.31 | ||
| 37 | 488.6 | 42.29 | 458.36~518.84 | 38 | 510.9 | 47.55 | 476.88~544.92 | ||
| 39 | 516.4 | 39.96 | 487.81~544.99 | 40 | 518.8 | 46.43 | 485.59~552.01 | ||
| 41 | 495.9 | 36.89 | 469.53~522.27 | 42 | °526.4 | 42.78 | 495.80~557.00 | ||
| 43 | 505.8 | 53.84 | 467.30~544.30 | 44 | 503.0 | 47.33 | 469.14~536.86 | ||
| 45 | 504.8 | 47.77 | 470.62~538.98 | 46 | 492.4 | 29.20 | 471.52~513.28 | ||
| 47 | 505.5 | 38.32 | 478.08~532.92 | 48 | 486.5 | 52.98 | 448.59~524.41 | ||
| 49 | 515.2 | 38.69 | 487.51~542.89 | 50 | 487.0 | 53.75 | 448.55~525.45 | ||
| 51 | 503.3 | 51.54 | 466.43~540.17 | 52 | 491.0 | 58.47 | 449.18~532.82 | ||
| 53 | 522.3 | 65.01 | 475.79~568.81 | 54 | 490.3 | 49.92 | 454.58~526.02 | ||
| 55 | 516.7 | 37.26 | 490.05~543.35 | 56 | 489.6 | 31.41 | 467.14~512.06 | ||
| 57 | 490.0 | 62.90 | 445.01~534.99 | 58 | 489.2 | 30.91 | 467.09~511.31 | ||
| 59 | 509.1 | 40.51 | 480.12~538.08 | 60 | 513.5 | 29.18 | 492.62~534.38 | ||
| 61 | 476.4 | 42.06 | 446.32~506.48 | 62 | 511.5 | 28.46 | 491.14~531.86 | ||
| 63 | 480.7 | 44.83 | 448.62~512.78 | 64 | 501.4 | 29.00 | 480.66~522.14 | ||
| 65 | 481.1 | 50.65 | 444.86~517.34 | 66 | 496.0 | 36.53 | 469.87~522.13 | ||
| 67 | 489.2 | 44.20 | 457.58~520.82 | 68 | 494.8 | 29.73 | 473.54~516.06 | ||
| 69 | 497.2 | 68.49 | 448.21~546.19 | 70 | 504.1 | 35.13 | 478.95~529.25 | ||
| 71 | 507.9 | 34.35 | 483.33~532.47 | 72 | °465.3 | 25.56 | 447.02~483.58* | ||
| 73 | 502.6 | 45.54 | 470.03~535.17 | 74 | 486.4 | 48.51 | 451.70~521.10 | ||
| 75 | °526.6 | 32.68 | 503.10~550.10* | 76 | 503.2 | 47.18 | 469.45~536.95 | ||
| 77 | 496.7 | 33.45 | 472.77~520.63 | 78 | 504.8 | 43.52 | 473.67~535.93 | ||
| 79 | 490.2 | 58.07 | 448.67~531.73 | 80 | 486.6 | 26.60 | 467.57~505.63 | ||
| 81 | 506.1 | 28.48 | 485.72~526.48 | 82 | 513.7 | 29.28 | 492.75~534.65 | ||
| 83 | 481.5 | 29.78 | 460.19~502.81 | 84 | 491.2 | 44.73 | 459.22~523.18 | ||
| 85 | 515.7 | 25.78 | 497.26~534.14 | 86 | 513.9 | 64.62 | 467.69~560.11 | ||
| 87 | 496.4 | 23.82 | 479.37~513.43 | 88 | 507.4 | 45.14 | 475.10~539.70 | ||
| 89 | 479.1 | 44.15 | 465.52~528.68 | 90 | 498.9 | 30.16 | 477.32~520.48 | ||
| 91 | 503.7 | 53.90 | 465.16~542.24 | 92 | 495.9 | 30.86 | 473.78~518.02 | ||
| 93 | 494.6 | 58.48 | 452.78~536.42 | 94 | 507.1 | 42.44 | 476.74~537.46 | ||
| 95 | 488.5 | 36.15 | 462.65~514.35 | 96 | 489.1 | 68.01 | 440.44~537.76 | ||
| 97 | °530.1 | 58.72 | 488.09~572.11 | 98 | 518.7 | 45.10 | 486.44~550.96 | ||
| 99 | 507.8 | 41.87 | 477.85~537.73 | 100 | 540.6 | 55.17 | 465.13~544.07 | ||
已知按正态分布,理论上有95%的变量值分布在均数加、减1.96倍标准差(样本均数的标准差称标准误)的范围内,这里也即100个样本均数中有95个分布在500-1.96(13.60)=473.34至500+1.96(13.60)=526.66的范围内。现看表6.4,在100个样本均数中,第6号(546.7)、第72号(465.3)、第97号(530.1)在上述范围之外,第42号(526.4)及第75号(526.6)就在临界值附近,其余95个(若将第42及75号计算在内则为97个)样本均数在此范围之内,将实际分布与理论分布相对照见下表6.5。100个样本均数的实际分布与正态分布的理论基本符合。