
第二节 X2检验
X2(称卡方)检验用途较广,但主要用于检验两个或两个以上样本率或构成比之间差别的显著性,也可检验两类事物之间是否存在一定的关系。
一、两个率的比较
(一)X2检验的基本公式 下页末行的例3.1是两组心肌梗塞病人病死率的比较,见表3.5,其中对照组未用抗凝药。两组病人的病死率不同,抗凝药组为25.33%,对照组为40.8%。造成这种不同的原因可能有两种:一种是仅由抽样误差所致;另一种是两个总体病死率确实有所不同。为了区别这两种情况,应当进行X2检验。其基本步骤如下:
1.首先将资料写成四格表形式,如表3.6。
将每个组的治疗人数分为死亡与生存两部分,各占四格表中的一格,这些数字称为实际频数,符号为A,即实际观察得来的数字。
2.建立检验假设 为了进行检验,首先作检验假设:两种疗法的两总体病死率相等,为35%(即70/200),记为H0:π1=π2。即不论用或不用抗凝药,病死率都是35%,所以亦可以换一种说法:病死率与疗法无关。
上述假设经过下面步骤的检验后,可以被接受也可以被拒绝。当H0被拒绝时,就意味着接受其对立假设即备择假设H1。此例备择假设为两总体病死率不相等,记为H1:π1≠π2
因为我们观察的是随机现象,所以无论是接受或拒绝H0都冒有一定风险,即存在着错判的可能性。一般要求,当错误地被拒绝的概率α不超过一定的数值,如5%(或0.05),此值称为检验水准,记为α=0.05。
3.计算理论频数 根据“检验假设”推算出来的频数称理论频数,符号为T。计算方法如下:假设两总体病死率相同,都是35.0%,那么抗凝血组治疗75人,其死亡的理论频数应为75×35.0%=26.25人,而生存的理论频数为75-26.25=48.75人。用同样方法可求出对照组的死亡与生存的理论频数,前者为43.75人。后者为81.25人。 然后,把这些理论频数填入相应的实际频数格内,见表3.6括号内数字。
计算理论频数也可用下式(3.4)
TRC=nRnC/N (3.4)
式中,TRC为R行与C列相交格子的理论频数,nR为与计算的理论频数同行的合计数,nC为与该理论频数同列的合计数,N为总例数。
例如;表3.6第一行与第一列相交格子的理论频数(T11)为
T11= 75×70/200=26.25
用两种方法计算,结果是相同的。
4.计算χ2值,计算χ2值的基本公式为:
X2=∑(A-T)2/t (3.5)
式中,A为实际频数,T为理论频数,∑为求和符号。
将表3.6里的实际频数与理论频数代入式(3.5)即求得χ2值。此例χ2=4.929。
从式3.5中可看出,实际频数与理论频数之差(A-T)愈小,所得的χ2值就愈小,理论频数是根据检验假设推算出来的,若与实际频数相差不大,说明假设与实际情况符合,于是就接受H0,认为两病死率无显著差别;反之,若(A-T)大,则χ2值亦大,说明假设与实际不符,就拒绝假设,认为两病死率有差别。但χ2值大还是小,要有一个比较的标准,要查χ2值表(附表1),查χ2值表前先要定自由度。
5.求自由度 自由度是数学上的一个名词。在统计中,几个数据不受任何条件(如统计量,即样本特征数)的限制,几个数据就可以任意指定,称为有几个自由度。若受到P个条件限制,就只有n-p个自由度了。例如在四格表中有四个实际频数,如没有任何条件限制,则4个数字都可任意取值,有4个自由度,当a+b,,c+d,a+c,b+d都固定后,在a、b、c、d四个实际频数中,只能有一个频数可任意指定了,因此,四格表的自由度为1。其计算公式为:
ν=(R-1)(C-1) (3.6)
式中,ν为自由度,R为横行数,C为纵列数。
四格表有2行和2列(注意:总计与合计栏不算在内)。因此ν=(2-1)(2-1)=1。
6.求P值,作结论 根据自由度查χ2值表(附表1)。此表的左侧ν为自由度,表内数字χ2值,表的上端P是从同一总体中抽得此样本χ2值的概率。三者关系是:在同一自由度下,χ2值越大,从同一总体中抽得此样本的概率P值越小;在同一P值下,自由度越大,χ2值也越大。χ2值与概率P呈相反的关系。χ2检验的常用界值为:
χ2<χ20.05()P>0.05 在α=0.05水准处接受H0,差别不显著
χ20.05≤χ2<χ20.01()0.05≥P>0.01 在α=0.05水准处拒绝HO,接受H1,差别显著
χ2≥χ20.01()P≤0.01 在α=0.01水准处拒绝HO,接受H1,差别显著
这里α是预定的检验水准。χ20.05()是当自由度为ν时与P=0.05相对应的χ2 值,简称5%点,χ20.01()是与P=0.01相对应的χ2 值,简称1%点。
当ν=1时,χ20.05(1)3.84,χ20.01(1)=6.63。本例自由度为1,求得χ2=4.929,介于3.84与6.63之间,或写成χ20.05(1)<χ2<χ20.01(1)。由于与3.84对应的纵行P=0.05,与6.63对应的纵行P=0.01,因此与样本χ2=4.929相应的概率介于0.05与0.01之间,写成0.05>P>0.01。在α=0.05水准处拒绝H0,接受H1,两总体率不等。对照组的病死率较抗凝血组高。
在α=0.05水准处拒绝H0,说明若在同样情况下作100次判断,将有5次或不到5次的机会,将原没有差别的两总体率错判为有差别,或说这样判断犯I型错误的概率不超过5%。
下面将实例的检验步骤集中列出。
例3.1 两组心肌梗塞病人的病死率可见于表3.5,其中对照组未用抗凝药。抗凝血组病死率为25.33%,对照组为40.80%,问两组病死率有无显著差别?
表3.5 两组心肌梗塞病人病死率比较
| 组别 | 治疗人数 | 死亡人数 | 病死率(%) |
| 抗凝血组 | 75 | 19 | 25.33 |
| 对 照 组 | 125 | 51 | 40.80 |
| 总 计 | 200 | 70 | 35.00 |
检验步骤如下:
1.将资料列成四格表形式,如表3.6。
表3.6 四格表式样
| 死亡 | 生存 | 合计 | |
| 抗凝血组 | 19(26.25) | 56(48.75) | 75 |
| 对照组 | 51(43.75) | 74(81.25) | 125 |
| 总 计 | 70 | 130 | 200 |
2.H0:两疗法的总体病死率相同,即π1=π2
H1:两疗法的总体病死率不同,即π1≠π2
α=0.05
3.求理论频数
抗凝血组:
死亡人数为75×35.0%=26.25人
存活人数为 75-26.25=48.75人
对照组:
死亡人数为125×35.0%=43.75人
存活人数为 125-43.75=81.25人
把理论频数填入相对应的实际频数格内,见表3.6括号内数字。
4.求χ2值 将表3.6里的数值代入式(3.5)得,

5.求自由度,确定P值,作结论
ν=(2-1)(2-1)=1,χ2 0.05(1)=3.84,χ2 0.01(1)=6.63,
本例χ2 =4.929,χ2 0.05(1)<χ2 <χ2 0.01(1),则0.05>P>0.01,在α=0.05水准处拒绝H0,接受H1,即两总体病死率不等,对照组病死率较抗凝血组高。
上例告诉我们,两个样本病死率一大一小,在未作检验之前,很难说它们两总体率是否有差别,为了作出正确判断,作X2检验。先假设两总体病死率相同,推算理论频数,由实际频数与理论频数计算χ2值,二者相差越大,χ2值也越大。本例得χ2=4.929,根据自由度为1时的χ2分布推断,从同一总体内抽样,出现χ2值等于或大于4.929的概率较小,每一百次中在5次以下,1次以上,因此检验假设被拒绝,而判断为有显著差别。
(二)连续性校正公式 χ2检验是以连续的光滑曲线做根据的,当自由度为1时,χ2检验所得的概率容易偏低,因些需要校正,校正后的χ2值比不校正的小一些,校正公式是:
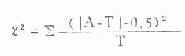 (3.7)
(3.7)
公式中A-T前后两条直线是绝对值的符号。
将表3.5资料代入式(3.7)得:
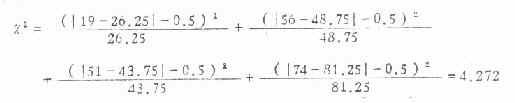
检验两个率相差的显著性时(此时自由度为1),理论上都可用校正公式。但当用公式(3.5)求出的χ2值小于3.84时,相应的P值大于0.05,表示两个率相差不显著,校正后χ2值更小,仍得同样结构,就无须校正;当用未校正公式求出的χ2值远远超过3.84时,校正后的结论仍相同,在此种情况下也可不校正;当自由度为2及以上时,则不必校正。
当用公式(3.5)求出的χ2值略大于3.84时,校正最为必要,往往会改变原来的结论,举例如下。
例3.2表3.7是六六六粉的两种配方进行野外烟剂灭黄鼠实验的观察结果。
表3.7 六六六粉两种配方灭黄鼠的效果
| 烟薰后鼠洞情况 | 合 计
(实验观察洞数) |
灭洞率
(%) |
||
| 未盗开 | 盗 开 | |||
| 04号配方 | 13(16.63) | 9(5.37) | 22 | 59.1 |
| 05号配方 | 80(76.37) | 21(24.63) | 101 | 79.2 |
| 总 计 | 93 | 30 | 123 | 75.6 |
现用公式(3.5)及式(3.6)分别计算χ2值如下:

校正后的χ2值小于3.84,P>0.05,在α=0.05的水准处接受H0,认为两种配方灭黄鼠效果无显著差异,这相结论是比较合理的,如果不经校正就会得出错误的结论。
(三)四格表中求χ2的专用公式 用上述基本公式(3.5)求χ2值,需要求出与实际频数一一对应的理论频数,运算较繁。在四格表中,用下列专用公式较为简便。
 (3.8)
(3.8)
式中a、b、c、d为四格表中的实际频数,N表示总例数(即N=a+b+c+d)。
现仍以表3.5资料为例,先写成四格表形式,如表3.8。
表3.8 四格表求χ2值专用公式的符号
| 死 亡 | 生存 | 合 计 | |
| 抗凝血组 | 19(a) | 56(b) | 75(a+b) |
| 对照组 | 51(c) | 74(d) | 125(c+d) |
| 70(a+c) | 130(b+d) | 200(N) |
将实际频数代入式(3.8)得,
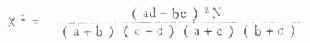
这里用专用公式求得的χ2值与前面用基本公式求得的结果完全不同,有时这两个公式求得的结果小数点后几位可能稍有出入,这是由于受小数四舍五入的影响。
前面已介绍了连续性校正公式(3.7),为使运算更为简便,下面列出专用公式的连续性校正公式(3.9),并以表3.8资料代入计算如下:
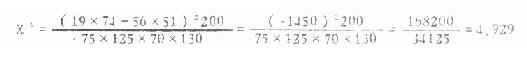 (3.9)
(3.9)
所得结果与式(3.7)求得的一致。
二、多个率或多个构成比的比较
(一)2×K表的专用公式,前面已讨论了,两个率的比较用四格表专用公式计算χ2值较为简便。如果是多个率比较,就要列成2×K表。这里的K暂为所比较的组数,2为每个组内所划分的类型数。求χ2值时本可用基本公式计算,但以用下列专用公式为便:
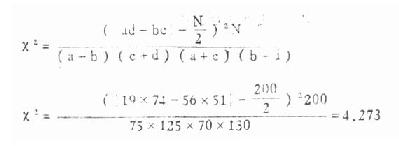 (3.10) (3.11)
(3.10) (3.11)
表3.9 2×K表形式之一
| a1
a2 ┆ ┆ |
b1
b2 ┆ ┆ |
n1
n2 ┆ ┆ |
| ∑ai | ∑bi | N |
公式中符号的意义参阅表3.9,以上两个公式的计算结果是完全一样的。
例3.3 某地观察磺胺三甲氧吡嗪加增效剂(吡嗪磺合剂)预防疟疾复发的效果,用已知有抗疟疾复发效果的乙胺嘧啶和不投药组作对照,比较三组的疟疾复发率,资料如表3.10,问三组复发率有无显著差别?
表3.10 三个组的疟疾复发率
| 组 别 | 观察例数 | 复发例数 | 复发率(%) |
| 吡嗪磺合剂
乙胺嘧啶 对 照 |
1996
473 484 |
76
27 53 |
3.81
5.71 10.95 |
| 合 计 | 2953 | 156 | 5.28 |
χ2检验步骤如下:
1.将表3.10资料写成2×K表形式,见表3.11。注意:这里必须把各组的观察例数分为复发和未复发两部分,这样表3.10就为写成2×3表。
表3.11 三个组疟疾复发率的比较
| 复发 | 未复发 | 合 计 | |
| 吡嗪磺合剂 | 76 | 1920 | 1996 |
| 乙胺嘧啶 | 27 | 446 | 473 |
| 对 照 | 53 | 431 | 484 |
| 合 计 | 156 | 2797 | 2953 |
2.H0:三个总体复发率相同
H1:三个总体复发率不全相同
α=0.05
3.求χ2值 将表3.11的数值代入式(3.10)(因为在表3.11中,各组的a值较小,计算较方便)得:
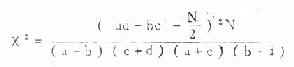
4.求自由度,确定P值,作结论
ν=(K-1)(2-1)=(3-1)(2-1)=2,查χ2值表得χ20.01(2)=9.21,本例χ2=39.92>χ20.01(2),P<0.01,在α=0.05的水准处拒绝H0,接受H1,即三个组的复发率有显著差别。
本例的结论是三个组的复发率有显著差别,因此,还需进一步说明三组中那两组有差别,可用四格表对每两个率进行假设检验。本例的检验结果是:吡嗪磺合剂与对照组比(P<0.01),乙胺嘧啶组与对照组比(P<0.01),而吡嗪磺合剂与乙胺嘧啶比(P>0.05),说明吡嗪磺合剂有预防疟疾复发的作用,其效果不低于乙胺嘧啶。
本例2×K表的2是指得发、未复发两项,K为比较的组数,K=3。如果比较组数只有2,而构成每组的项数则多于2,如甲状腺肿的型别构成可分为弥漫型、结节型、混合型三种。这类资料亦同样可用2×K表专用公式进行检验。这时把2作为比较组数,K作为项数,检验方法同上,表3.12是2×K表的另一种形式。
表3.12 2×K表形式之二
| a1 | a2 | …… | ∑ai
∑bi |
| b1 | b2 | …… | |
| n1 | n2 | …… | N |
例3.4,为研究不同地域甲状腺型别的构成有无显著差别,某省对两个县的居民进行甲状腺肿调查,得资料如表3.13,问甲乙两县各型甲状腺肿患者构成比有无显著判别?
表3.13 某省甲乙两县甲状腺肿患者型别构成比较
| 县名 | 弥漫型 | 结节型 | 混合型 | 合计 |
| 甲县 | 486 | 2 | 4 | 492 |
| 乙县 | 133 | 260 | 51 | 444 |
| 合计 | 619 | 262 | 55 | 936 |
检验步骤如下:
1.H0:两总体甲状腺肿型别构成相同
H1:两总体甲状腺肿型别构成不同
α=0.05
2.求χ2值, 将表3.13中的数值代入式3.10得:
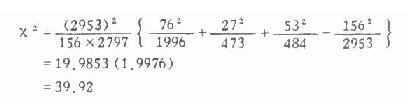
3.求自由度,确定P值,作结论。
ν=(3-1)(2-1)=2,查χ2值表得χ20.01(2)=9.21,本例,χ2=494.36,P<0.01,在α=0.05水准处拒绝H0,接受H1,甲、乙两县甲状腺肿型别构成有差别(P<0.01)。甲县以弥漫型为主,而乙县结节型较多,地域与患者的型别构成具有一定的关系。
此类资料经χ2检验作结论,如果不显著,说明两组资料的构成比来自同一总体,没有显著差别。如果结论显著,说明两组的构成比来自不同总体,差别有显著性。同时要指出两组构成的主要区别。
(二)R×C表的通用公式当资料的行数和列数都超过2时称R×C表。对此种资料作假设检验时,可用基本公式(3.5),但运算较繁,如果用R×C表的通用公式计算χ2值,较为简便。
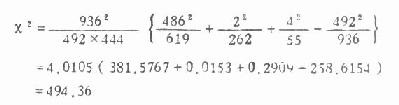 (3.12)
(3.12)
式中,Aij为i行第j列的实际频数,ni为第i行的合计数,nj为第j行列的合计数,N为总频数。
这个公式也系由基本公式(3.5)推导出来,式(3.12)也可用以求四格表、2×K表资料的X2值,故称通用公式,用此公式不需计算理论频数,与基本公式(3.5)相比,较为简便。
例3.5某院肝胆外科在手术中观察了胆结石的部位与类型得资料如表3.14,试分析两者间有无关系存在?
表3.14 胆结石类型与部位的关系
| 结石部位 | 总例数 | 例 数 | 百 分 比 | ||||
| 胆固醇结石 | 胆红素结石 | 其它 | 胆固醇结石 | 胆红素结石 | 其它 | ||
| 胆囊 | 118 | 70 | 16 | 32 | 59.3 | 13.6 | 27.1 |
| 肝外胆管 | 75 | 12 | 39 | 24 | 16.0 | 52.0 | 32.0 |
| 肝内胆管 | 29 | 2 | 20 | 7 | 6.9 | 69.0 | 24.1 |
| 合计 | 222 | 84 | 75 | 63 | 37.8 | 33.8 | 28.4 |
检验步骤如下:
1.将表3.14资料写成R×C表形式,见表3.15.
表3.15 胆结石类型与部位的关系
| 结
石 部 位 |
结 构 类 型 | ||||
| 胆固醇结石 | 胆红素结石 | 其它 | 合计 | ||
| 胆囊 | 70 | 16 | 32 | 118 | |
| 肝外胆管 | 12 | 39 | 24 | 75 | |
| 肝内胆管 | 2 | 20 | 7 | 29 | |
| 合计 | 84 | 75 | 63 | 222 | |
2.H0:胆结石的类型与部位没有关系
H1:胆结石的类型与部位有关系
α=0.01
3.求χ2值 将表3.15数值代入式(3.12)得:

4.求自由度,确定P值,作结论。
ν=(3-1)(3-1)=4,查χ2值表得χ20.01(4)=13.28,本例χ2=64.06<χ20.01。在α=0.01水准处拒绝H0,接受H1,胆结石类型与部位有显著关系存在(P<0.01),胆囊内以胆固醇结石居多,肝内、外胆管以胆红素结石为主。